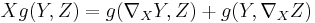Metric connection

In mathematics, a metric connection is a connection in a vector bundle E equipped with a metric for which the inner product of any two vectors will remain the same when those vectors are parallel transported along any curve. Other common equivalent formulations of a metric connection include:

A connection for which the covariant derivatives of the metric on E vanish.
A principal connection on the bundle of orthonormal frames of E.

A special case of a metric connection is the Levi-Civita connection. Here the bundle E is the tangent bundle of a manifold. In addition to being a metric connection, the Levi-Civita connection is required to be torsion free.

Riemannian connections

An important special case of a metric connection is a Riemannian connection. This is a connection 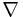$\nabla$ on the tangent bundle of a pseudo-Riemannian manifold (M, g) such that 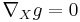$\nabla_X g = 0$ for all vector fields X on M. Equivalently, 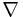$\nabla$ is Riemannian if the parallel transport it defines preserves the metric g.

A given connection 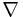$\nabla$ is Riemannian if and only if

$Xg(Y,Z)=g(\nabla_XY,Z)%2Bg(Y,\nabla_XZ)$

for all vector fields X, Y and Z on M, where 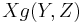$Xg(Y,Z)$ denotes the derivative of the function 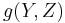$g(Y,Z)$ along this vector field $X$ .

The Levi-Civita connection is the torsion-free Riemannian connection on a manifold. It is unique by the fundamental theorem of Riemannian geometry.

External links

a pdf about this